\[y=\frac{ax+b}{cx+d}\]
, we can find the equations of the asymptotes using long division and rearranging into the form \[(x-x_0)(y-y_0=K\]
. The asymptotes are then \[x=x_0, \; y=y_0\]
. If \[K \gt 0\]
the hyperbola is in the 1st and 3rd quadrant and if \[K \lt 0\]
the hyperbola is in the 2nd and 4th quadrant.
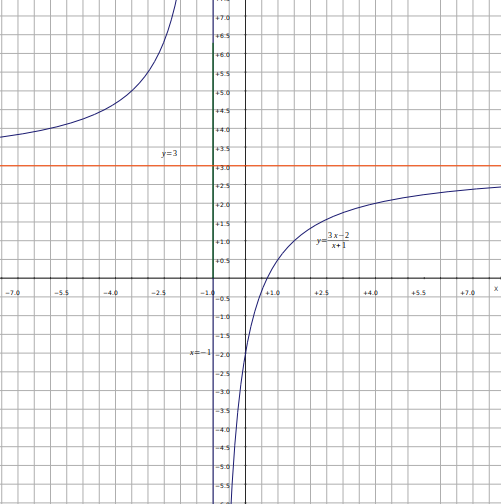
Example: \[y=\frac{3x-2}{x+1}\]
.Long division gives
\[y=3- \frac{5}{x+1}\]
.Subtract 3 to give
\[y-3=- \frac{5}{x+1}\]
.Multiply by
\[(x+1)\]
to give \[(x+1)(y-3)=-5\]
.The asymptotes are
\[x=-1, \; y=3\]
and the hyperbola is in the 2nd and 4th quadrant.