If some quantity is increasing decreasing by the same proportion or factor in each time interval, then it is said to vary exponentially. A good example is money left in a bank which attracts compound interest at the same rate each year. If the rate of interest is 5%, then at the end of every year the amount of money in the bank is multiplied by 1.05 (
). If the amount of money in the bank is initially
then the amount after
years is
This equation is of the form
where
and
are constants.
We may know that a quantity
varies exponentially, so be able to write
whereandare constants. We want to find the constantsand
Suppose that
when
and
when
Substituting these values into the expression for Q gives
for
(1)
for
(2)
(2) dividing by (1) gives
Then from (1)
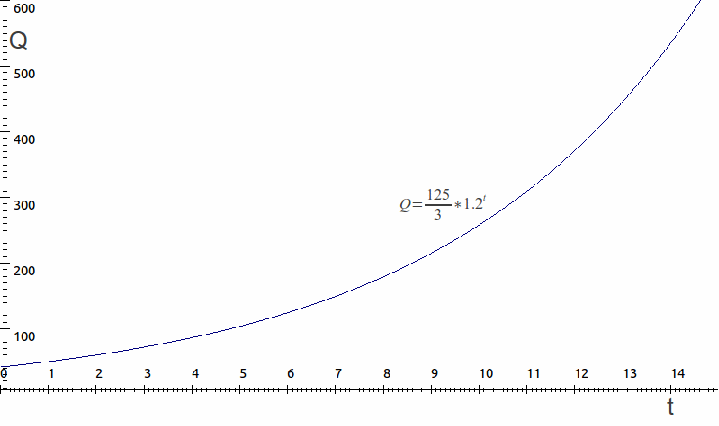
Then
The graph ofagainst
is given below. Notice how the graph curls upwards.
