Given a linear transformation A , a non-zero vector x is defined to be an eigenvector of the transformation if it satisfies the eigenvalue equation
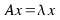 (1)
(1) - for some scalar
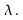 In this situation, the scalar
In this situation, the scalar is called an "eigenvalue" of A corresponding to the eigenvector
is called an "eigenvalue" of A corresponding to the eigenvector In other words the result of multiplying
In other words the result of multiplying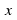 b y the matrix is just a scalar multiple
b y the matrix is just a scalar multiple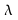 of
of
The key equation in this definition is the eigenvalue equation,![]() Most vectors
Most vectors![]() will not satisfy such an equation: a typical vector changes direction when acted on by A , so that
will not satisfy such an equation: a typical vector changes direction when acted on by A , so that![]() is not a multiple of
is not a multiple of![]() This means that only certain special vectors are eigenvectors, and only certain special scalars
This means that only certain special vectors are eigenvectors, and only certain special scalars![]() are eigenvalues. Of course, if A is a multiple of the unit matrix, then no vector changes direction, and all non-zero vectors are eigenvectors.
are eigenvalues. Of course, if A is a multiple of the unit matrix, then no vector changes direction, and all non-zero vectors are eigenvectors.
The requirement that the eigenvector be non-zero is imposed because the equation![]() holds for every A and every
holds for every A and every![]() Since the equation is always trivially true, it is not an interesting case. In contrast, an eigenvalue can be zero in a nontrivial way. Each eigenvector is associated with a specific eigenvalue. One eigenvalue can be associated with several or even with an infinite number of eigenvectors by scaling a vector.
Since the equation is always trivially true, it is not an interesting case. In contrast, an eigenvalue can be zero in a nontrivial way. Each eigenvector is associated with a specific eigenvalue. One eigenvalue can be associated with several or even with an infinite number of eigenvectors by scaling a vector.

![]() acts to stretch the vector
acts to stretch the vector![]() not change its direction, so
not change its direction, so![]() is an eigenvector of A .
is an eigenvector of A .
From (1)![]() which we may factorise as
which we may factorise as![]() hence det
hence det![]() where I is the identity matrix.
where I is the identity matrix.
- We may then form a polynomial equation in
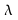 and solve it to find the eigenvalues:
and solve it to find the eigenvalues: - A=
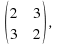 A-λI=
A-λI=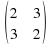 -
- 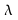
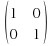 which becomes
which becomes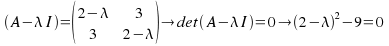 We can simplify, factorise and solve.
We can simplify, factorise and solve. -
-
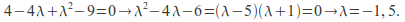
-
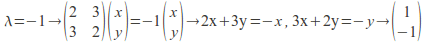 is an eigenvector.
is an eigenvector.
![]() is an eigenvector.
is an eigenvector.
