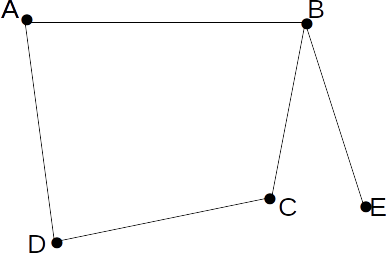
| A | B | C | D | E | |
| 0 | 1 | 1 | 1 | 1 | 0 |
| B | 1 | 0 | 1 | 0 | 1 |
| C | 1 | 1 | 0 | 1 | 0 |
| D | 1 | 0 | 1 | 0 | 0 |
| E | 0 | 1 | 0 | 0 | 0 |
\[M= \left( \begin{array}{ccccc} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{array} \right)\]
.A liaison official whose removal from a connected graph results in a disconnected graph, or equivalently result in two other officials being not able to communicate. The above graph is connected since there is a route from any vertex to any other vertex with no repeated vertex. A graph with n vertices if and only if the matrix
\[M+M^2+...+M^{n-1}\]
has no zero elements.If vertex A is removed the incidence matrix becomes
\[M_1= \left( \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{array} \right)\]
.\[M_1+M^2_1+M^3_1= \left( \begin{array}{cccc} 2 & 4 & 1 & 3 \\ 4 & 2 & 3 & 1 \\ 1 & 3 & 1 & 1 \\ 3 & 1 & 1 & 1 \end{array} \right) \]
.There are no zero entries so A is not a liaison official. Similarly for C, D and E. B is a liaison official because the same process for B does result in a matrix with zero entries. From the graph, if B is removed, E cannot communicate with anyone else.
