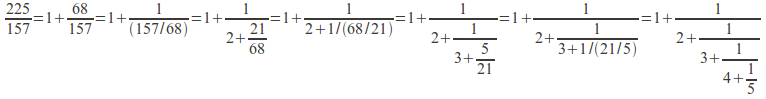Introduction to Continued Fractions

Letbe any real number and letbe any positive real numbers. The expression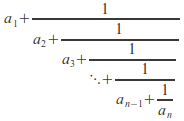

is called a finite continued fraction and the numbersare partial quotients of the continued fractions. When all the partial quotients are integers the partial fraction is said to be simple. The partial fraction above is written

Example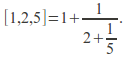

The definition gives rise to the identityThis identity is called The First Continued Fraction Identity.

It is obvious that any simple finite continued fraction is a rational number. Conversely any rational number can be expressed as a finite continued fraction using the Euclidean Algorithm.

Example: Find a finite continued fraction for

Then