Properties of Euler's Totoent Function

Euler's totient function is defined asie the number of positive integers less than or equal torelatively prime to

The function has the following properties:

a)

b)(1) where

c)if

d)dividesimpliesdivides

e)is even forAlso ifhasdistinct odd prime factors then divides

Proof:

a)We can putin the formula for:

b)Note that each prime divisor of mn is either a prime divisor of m or of n, and those primes which divide both m and n also divide gcd(m,n). Hence

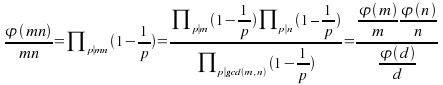
From which we get (1) on multiplying by

c)Putin (1)

d)We deduce d) from b). Sincedivideswe can writewhereIfthen and d) is satisfied, so assumeandthen from b)(2) whereNow use induction onis trivial. Suppose d) holds for allthen it holds forsosinceThen the right hand side of (2) is a multiple ofwhich means that

e)Ifa) shows thatis even. If n contains at least one odd prime factor we writewhereThe coefficient ofis even sois even. Each prime factor contributes a factor 2 to this coefficient soifhasdistinct odd prime factors.