Probability Generating Functions

The probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable.

Ifis a discrete random variable taking values in the non-negative integersthen the probability-generating function ofis defined as

whereis the probability mass function of

If is a discrete random variable taking values in the d-dimensional non-negative integer latticethen the probability-generating function ofis defined as

whereis the probability mass function of X. The power series converges absolutely for all complex vectorswith

Probability generating functions obey all the rules of power series with non-negative coefficients.

The following properties allow the derivation of various basic quantities related to

1. The probability mass function ofis recovered by taking derivatives of

2. If two probability distributions has the same probability generating function then they are the same distribution.

The expectation ofis given bywhereindicatesfrom below.

More generally, the kth factorial moment,of X is given bySo the variance of X is given by

3.whereis a random variable,is the probability generating function andis the moment-generating function.

Probability-generating functions are useful when several independent random variables are involved. For example:

• If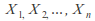is a sequence of independent random variables, and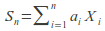

where the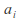are constants, then the probability-generating function is given by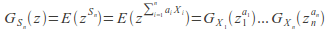

For example, if S-n =SUM^n-{i=1} X-i then

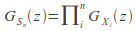
It follows that the probability-generating function of the difference of two independent random variable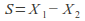sis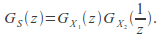

Example:

• The probability-generating function of a constant random variable, i.e. one with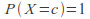is

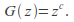
• The probability-generating function of a binomial random variable, the number of successes in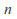trials, with probability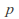of success in each trial, is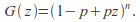

• The probability-generating function of a negative binomial random variable, the number of failures occurring before the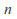th success with probability of success in each trial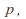is

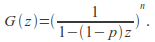
Note that this is the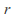th power of the probability generating function of a geometric random variable.

• The probability-generating function of a Poisson random variable with rate parameter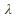is