Normal Probability Plots - Testing for Normality

Suppose we have n observations– which we assume are in ascending order - and we want to know whether they could have arisen from a normal distribution. We plot the data points against the corresponding standard normal quantilesgiven byforIf the data is from a normal population then the pointsshould lie approximately on a straight line. This is called a normal probability plot and is especially suited to small data sets.

Example:

We have some silver coins from ancient Byzantine. We want to test whether the % silver content follows a normal distribution.

First arrange the data in order.

Now find the quantiles:etc.

Plot the points

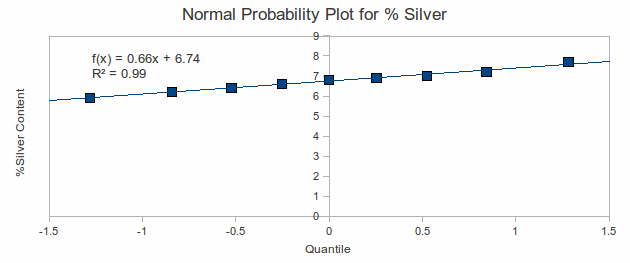
The correlation coefficient () indicates a very good fit to a straight line, hence we may take the silver content as normally distributed.