The Mann – Whitney – Wilcoxon test may be used to test the hypothesis that two independent samples A and B arise from the same population. The test is very nearly as powerful as the two sample t – test, and may be used where the t – test may not because of lack of normaility. The procedure is:
-
Pool the two samples and sort the combined data into ascending order, simultaneously keeping track of which data belongs to which group.
-
Allocate a rank to each data value with the smallest being given rank one. If two ranks are equal, allocate the average of the two ranks to each.
-
Add up the ranks with
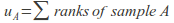and 
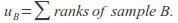Notice that if A has n-A data points and B has n-B data points then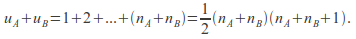
-
The Mann – Whitney – Wilcoxon test statistic is
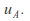Very small or large values for
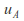imply rejection of the null hypothesis that the two samples are from the same population. - 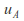is compared with values of the null distribution of 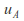taken from a table.
Example: Suppose men and women run a 800m race.
The men finish in times 1.50.32,1.54.45,1.57.54,2.00.23,2.01.23 and 2.45.43.
The women finish in times 1.50.10.2.07.45,2.09.54,2.10.23,2.21.23 and 2.25.43.
Sorting these in order, with the labels M for men and W for women we have WMMMMMWWWWWM.
The sum of the ranks for the men is
so
At the 5% level the rejection region is
The null hypothesis is rejected.