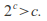Cardinality

The cardinality of a setwrittenis a measure of the "number of elements of the set". The cardinality of a finite set is equal to the number of elements of the set. For infinite sets cardinality is measured using either bijections/injections or cardinal numbers.

Two sets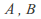have the same cardinality if there exists an injective (one to one) and surjective (onto) function from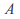to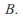The set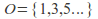of odd natural numbers has the same cardinality as the set of natural numbers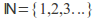with the function fromtogiven by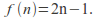All infinite countable sets have the same cardinality asthe smallest set with infinite cardinality

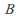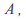If there exists an injective function fromtothen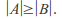If there is an injective but no bijective function then the cardinality of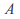is greater than the cardinality of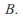The cardinality of the set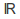of real numbers is greater than the cardinality of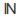for this reason.

The cardinality of a set can be defined in terms of equivalence relations. The equivalence classof a set A under this relation then consists of all those sets which have the same cardinality as A.

WE check that the equivalence axioms are satisfied:

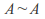1. since the identity function from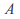to itself is bijective and surjective.

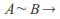2. there exists an injective and surjective function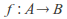and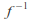is well defined becauseis injective and surjective hence

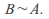
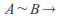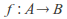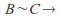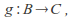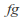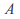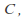3. there exists an injective and surjective functionandthere exists an injective and surjective functionsois an injective and surjective function fromtoso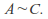

Any setwith cardinality less than is said to be a finite set.

Any setthat has the same cardinality as is a countably infinite set.

Any setwith cardinality greater thanis said to be uncountable.

The cardinality of the continuum () is greater than that of the natural numbers (); that is, there are more real numbersthan whole numbers

Because for any open intervalin there exists a bijection (eg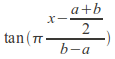from that interval ontothe cardinality ofis equal to the cardinality of any open interval inCardinal arithmetic can be used to show not only that the number of points inis equal to the number of points in any open interval ofand to the number of points on a plane and, indeed, infor any

That the cardinal number ofis equal to the cardinal number ofmay be demonstrated with the use of space filling curves, which demonstrate a bijection fromto

The set of all subsets of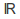and the set of all functions from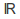to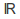both have cardinality