Constructing ZDDs

Given a family  
\[F\]
  of sets, we can find its ZDD as follows.
  • If  
    \[F = \emptyset\]
      (
    \[F\]
      is empty) return  
    \[\bot\]
     . If  
    \[F = \epsilon\]
      (
    \[F\]
      contains only the empty set) then return  
    \[\top\]
     .
  • Find the smallest element  
    \[v\]
      amongst all elements in all sets of  
    \[F\]
     . Create a node  
    \[v\]
     .
  • Let  
    \[F_0\]
      be the family of all sets in  
    \[F\]
      not containing  
    \[v(\]
    , that is,  
    \[; F_0 = \{ \alpha : \alpha \in F, v \notin \alpha \}\]
    . Recursively construct the ZDD for  
    \[F_0(\]
    , and connect the LO edge from  
    \[v\]
      to the root of  
    \[F_0\]
     .
  • Let  
    \[F_1\]
      be the family resulting from taking all sets in  
    \[F\]
      that contain  
    \[v\]
      and then removing  
    \[v\]
      from each set:  
    \[ F_1 = \{ \alpha\setminus\{v\} : \alpha \in F, v \in \alpha \} \]
    . Recursively construct the ZDD for  
    \[F_1\]
    , and connect the HI edge from  
    \[v\]
      to the root of  
    \[F_1\]
     .
  • Look for identical nodes (same label, same LO desination and same HI destination) and combine them.
    • Some families have special properties allowing their ZDDs to be immediately constructed. In a universe of size  
    \[n\]
    , consider for example the family of all sets of size  
    \[k\]
      which we denote  
    \[S_k(\{1,...,n\})\]
     . The ZDD of  
    \[S_2(\{1,2,3\}) = \{ \{1,2\}, \{2,3\}, \{1,3\}\}\]
      is the following: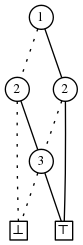

    con1.png

    The ZDD of  
    \[S_k(\{1,...,n\})\]
      turns out to be easy to describe (exercise).
    Here are some more examples. Let  
    \[U = \{1, ..., 6\}\]
      and  
    \[S = \{2,3,5\}\]
     . The ZDD of all subsets of  
    \[U\]
      containing exactly one element of  
    \[S\]
      is: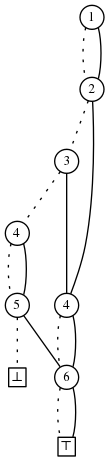

    con2.png

    The ZDD of all sets containing at least one element of  
    \[S\]
      is:

    con3.png

    The ZDD of all sets containing at most one element of  
    \[S\]
      is:

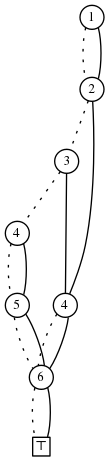
    con4.png

    These 3 examples are readily generalized. Each can be viewed as a ZDD of all sets that branches off at the smallest element of  
    \[S(\]
    , before joining the main branch again after the largest element of  
    \[S\]
      has been handled.

    Add comment

    Security code
    Refresh