Countable Sets

A countable set is a set that can be matched one to one with some subset of the set of natural numbers. Every finite set is countable. A set that is not countable is called uncountable. For instance the set of all even numbers is countable, with the matching provided byand so is the set of all rational fractions with the mapping illustrated in the table below.

In exactly the same way the set of points in the xy plane with integer coordinates can be put in a one - to one correspondence with the set of natural numbers:

The correspondence generates a square spiral, shown below.

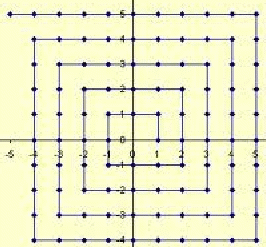
Henceis countable, and by induction so isand for

is not countable.

Proof: Assume thatis countable. Eachcan be expressed as an infinite decimal. Suppose the 1-to-1 correspondence withis :

such that every real number appears in the list on the right.

Choose a real numbersuch thatetc.

This real number is different from all those in the list, and hence there cannot exist such a 1-to-1 correspondence betweenand the whole ofsois uncountable.