Cosets

Ifis a group,is a subgroup ofandthen

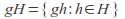is a left coset of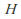in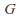

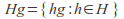is a right coset of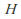in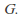

Ifor equivalentlyfor allthenis a normal subgroup ofThe left and right cosets coincide and the set of cosets forms a group with the group operation defined byForunder the operation addition modulo 3, the cosets ofareandIf G is abelian then all subgroups are normal.

if and only ifis an element of H since as H is a subgroup, it must be closed and must contain the identity.

Any two left cosets ofinare either identical or disjoint — i.e., the left cosets form a partition ofsuch that every element ofbelongs to one and only one left coset. In particular the identity is in precisely one coset, and that coset isitself since this is also the only coset that is a subgroup.

The left cosets ofinare the equivalence classes under the equivalence relation ongiven byif and only ifand similarly for right cosets.

All left cosets and all right cosets have the same order (number of elements, or cardinality in the case of an infinite H), equal to the order of H (because H is itself a coset). Furthermore, the number of left cosets is equal to the number of right cosets and is known as the index of H in G, written asLagrange's theorem allows us to compute the index in the case whereandare finite, as per the formula: