Conjugacy

Elementsandof a groupare called conjugate if there existssatisfying

Conjugacy is an equivalence relation since

1. so

2. so

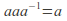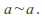
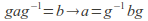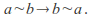
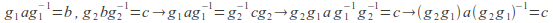3. so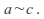

splits into equivalence classesEvery element of the group belongs to precisely one conjugacy class, and the classesandare equal if and only ifandare conjugate, and disjoint otherwise. The equivalence class that contains the elementisand is called the conjugacy class ofThe class number ofis the number of distinct (nonequivalent) conjugacy classes.

Elements of each conjugacy class have a similar structure. If the group elements act on a geometric object, elements of each conjugacy class have similar geometric effects. For example, all the rotations may form one class, all the reflections another, and the identity will be in a class by itself.

The symmetric groupconsisting of all 6 permutations of three labels, has three conjugacy classes:

• The identity (1)(2)(3).

• interchanging two two labels (12)(3), (13)(2),(1)(23).

• a cyclic permutation of all three labels (123), (132).

Ifis abelian, thenfor all sofor allso conjugacy is not very useful in the abelian case. A subset of the group may be abelian so the conjugacy classes gives us an idea of the extent of non – abelianness.

Ifbelong to the same conjugacy class - they are conjugate - then they have the same order and every statement aboutcan be translated into a statement aboutbecause the mapis an automorphism of

An elementlies in the centerofif and only if its conjugacy class has only one element, a itself. More generally, ifdenotes the centralizer ofi.e., the subgroup consisting of all elementssuch thatthen the indexis equal to the number of elements in the conjugacy class of(by the orbit-stabilizer theorem).

Ifare conjugate, then so are powers of them,since