The elements of any group may be partitioned into conjugacy classes. Two elements
of a group are in the same conjugacy class if there exists
such that
Conjugacy is an equivalence relation:
-
Since
-
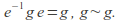
If
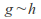then there exists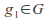such that
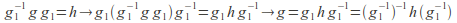hence h sim g. -
If
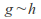and
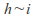then there exist
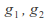such that
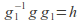and
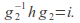then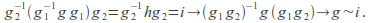
Hence the operation of conjugation divides the group into equivalence classes. Members of the same conjugacy class share many properties – they have the same order, if they are members of a permutation group, they have the same cycle structure for example. It does not follow that all elements of the same order or type fall in the same conjugacy class. In fact, for abelian groups every element
is in a conjugacy class all by itself, since
for all
Only non – abelian groups are of interest.
Example:
has three conjugacy classes:
From this we can write down the conjugacy class equation for
Each term in this equation in the number of elements in that conjugacy class. Since all the conjugacy classes are disjoint and their union is the group itself, the sum of the orders of the conjugacy classes is equal to the order of the group.
Example:
has 3 conjugacy classes
The conjugacy class equation for
is then 8=1+2+1+4.
Notice that the size of each conjugacy class is a divisor of the order of the group. This is a consequence of Lagrange's theorem, since the stabilizer of each conjugacy class is a subgroup, so divides the order of the group.