If the set of real numbers
is countable then there exists a one to one correspondence between the set of natural numbers
and
Conversely ifis not countable then no such one to one correspondence exists. We can prove that no such correspondence exists by showing that for each set of real numbers
a real number
exists which does not belong to the sequence.
Define a sequence of closed intervals
such that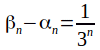
and
for
Divide the closed interval
into intervals of equal length
and
and choose one not containing
Call that interval
Divide
into three equal sets and choose one not containing
Call that interval
Keep going in the same manner until we have the closed interval 
of length
which does not contain the point
Letdenote the common intersection of all the intervals
for each
but
because
We have a sequence of real numbersnot containingso thatis not countable.