Equivalent Definitions of Compactness
Theorem
The following statements are equivalent:
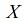is compact.For every family
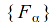of closed subsets of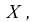
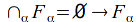contains a finite subclass
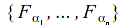such that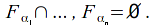
Proof
Suppose
then from De Morgans's Laws,
is an open cover ofbecause all the
are closed.
Sinceis compact a finite subcover
exists.
Again from De Morgans' Laws,
Conversely, let
be an open cover ofso that
where each
is open in
From De Morgans' Laws,
All the
are closed and have empty intersection. A subclass of
exists such that
Again using De Morgan's Laws,
andis compact.
