The genus of a surface is the greatest number of continuous non self intersecting closed curves which may be drawn on a surface without dividing it into distinct regions.
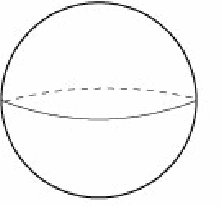
| A sphere has a genus of zero. Any curve drawn on the surface of a sphere will divide the sphere into two parts. An equator will divide the sphere into a top and a bottom. Any simply closed surface will no holes is homeomorphic the the sphere and has a genus of one. |
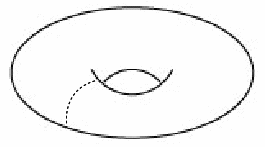
| A one holed torus has a genus of one. A curve can be drawn in the surface to cut the torus into a tube, but any pother closed curve will divide the tube into two tubes. |
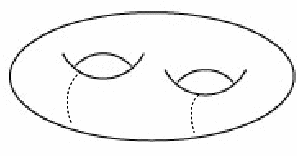
| A two holed torus has a genus of two. A curve can be drawn from each hole but if any other curves are drawn the torus will be disconnected. In general an n holed torus has a genus of n. |