A Hausdorff or![]() space is a topological space in which distinct points have disjoint neighbourhoods, implying that any two points are part of disjoint open sets.
space is a topological space in which distinct points have disjoint neighbourhoods, implying that any two points are part of disjoint open sets.![]() are Hausdorff with the usual topology because if
are Hausdorff with the usual topology because if![]() then
then![]() so each of
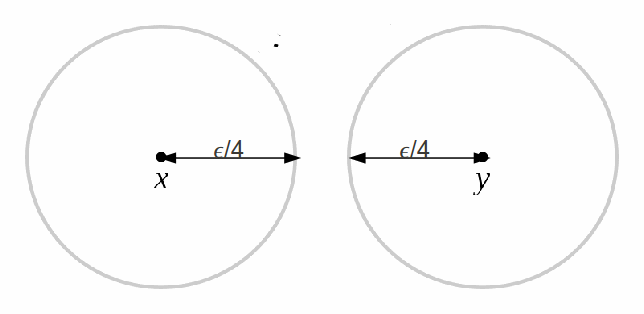
so each of![]() can be placed inside open balls of radius
can be placed inside open balls of radius![]()
The Hausdorff condition implies the uniqueness of limits of functions, since if![]() is continuous and
is continuous and![]() a sequence convergent to x so that
a sequence convergent to x so that![]() and
and![]()
![]() are subsequences of
are subsequences of![]() then for
then for![]() given there exists
given there exists![]() such that
such that![]() implies
implies![]()
Take![]()
Since![]() is convergent and f is continuous there exists
is convergent and f is continuous there exists![]() such that
such that![]() and similarly
and similarly![]() implies
implies![]() Hence
Hence![]()
Hence![]()
This is a contradiction hence limits of functions are unique. Since![]() is also a sequence, limits of sequences are unique.
is also a sequence, limits of sequences are unique.
