Homeomorphisms

A homeomorphism is a continuous function between two topological spaces that has a continuous inverse function. They preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and are the same topologically.

A topological space is a geometric object, and the homeomorphism is a continuous stretching and bending of the object. Thus, a square and a circle are homeomorphic to each other, but a sphere and torus are not. Any flat surface with no holes is homeomorphic to a square. Any three dimensional surface with a single hole is homeomorphic to the torus.

Topology is the study of those properties of objects that do not change when homeomorphisms are applied. Topology may be considered as the spacial properties of objects or the relationships between the spatial properties of different objects.

A functionbetween two topological spaces is called a homeomorphism if the following is true:

• is a bijection (one-to-one and onto)

• is continuous

• the inverse functionis continuous (is an open mapping, that is, sends open sets to open sets).

If such a function exists, X and Y are homeomorphic. The homeomorphisms form an equivalence relation on the set of all topological spaces. The resulting equivalence classes are called homeomorphism classes.

Examples

• The unit disk in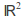and the unit square in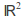are homeomorphic.

• The open interval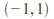is homeomorphic to the real numbers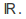

• The product space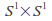and the two-dimensional torus are homeomorphic.

• The surface of a sphere in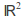with a single point removed is homeomorphic to the set of all points in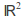(a 2-dimensional plane). The Riemann sphere with the operation of stereographic projection is an example.

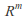• and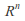are not homeomorphic for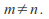The number of dimensions of a space is a topological property, preserved by homeomorphisms.