A Metric on a Cartesian Product of Metric Spaces

Letandrepresent metric spaces. We can define a metric spaceon the cartesian productby

forand

We testandin turn.

M1:andiff

and iff iffso M1 is satisfied.

M2:

so M2 is satisfied.

M3:

so M3 is satisfied andis a metric space.

Other possible metric spaces for a cartesian product exist – the discrete metric

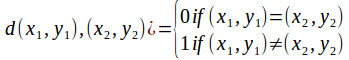
and the ordinary cartesian distance metric are examples.