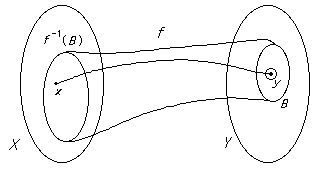
The map![]() between metric spaces is continuous if it satisfies the following properties, which are equivalent:
between metric spaces is continuous if it satisfies the following properties, which are equivalent:
- 1. For every open set
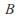 in
in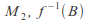 is open in
is open in
- This is the general topological definition of continuity.
- This means than if
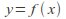 then an open set containing
then an open set containing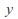 is sent to an open set containing
is sent to an open set containing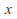 under
under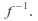
- 2. If
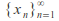 is a sequence in
is a sequence in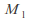 that converges to
that converges to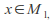 then the sequence
then the sequence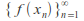 converges to
converges to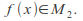
- 3. For every
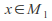 and every
and every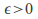 there exists
there exists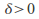 such that for all
such that for all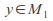 we have
we have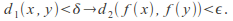 In general every space may have more than one possible metric. For fixed
In general every space may have more than one possible metric. For fixed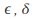 may depend on the metric chosen.
may depend on the metric chosen.
Moreover,![]() is continuous if and only if it is continuous on every compact subset of
is continuous if and only if it is continuous on every compact subset of![]()
The image of every closed set is closed, the image of every compact set under a continuous function is compact, and the image of every connected set under a continuous function is connected. It is not the case however that the image of every open set is open. If![]() is the constant map from
is the constant map from![]() to
to![]() with the Euclidean metric, then
with the Euclidean metric, then![]() is a single point hence is closed in
is a single point hence is closed in![]()
