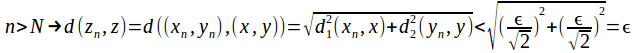Theorem
Suppose![]() and
and![]() are metric spaces. A sequence of points
are metric spaces. A sequence of points![]() of a metric space
of a metric space![]() is convergent to the point
is convergent to the point![]() if and only if
if and only if
![]() and
and![]()
Proof
Suppose![]() then there exists
then there exists![]() such that for
such that for![]() given such that for all
given such that for all![]() and if
and if![]() then there exists
then there exists![]() such that for
such that for![]() given such that for all
given such that for all![]()
Let![]() then
then ![]() and
and![]()
Hence