A topological space![]() is path connected if for each pair of points
is path connected if for each pair of points![]() there exists a continuous function
there exists a continuous function![]() from the unit interval
from the unit interval![]() to
to![]() with
with![]() and
and![]()
Path connectedness is an equivalence relation:
![]() since the constant map
since the constant map![]() is continuous.
is continuous.
![]() since if
since if![]() is continuous with
is continuous with![]() we can write
we can write![]() then
then![]() and
and![]() with
with![]() continuous by continuity of
continuous by continuity of![]()
![]() and
and![]() since if there exists
since if there exists![]() and
and![]() with
with![]() then we can define
then we can define
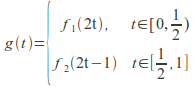
![]() is continuous since
is continuous since![]() and
and![]() so there exists a path in
so there exists a path in![]() from
from![]() to
to![]() and
and![]()
This equivalence relation splits![]() into path connected components.
into path connected components.
Every path-connected space is connected. The converse is not always true. The complex plane with infinity included is not path connected since![]() but there is no continuous function in
but there is no continuous function in![]() with
with![]() but
but![]()
![]() is path connected however.
is path connected however.
Subsets of the real line![]() are connected if and only if they are path-connected; these subsets are the intervals of
are connected if and only if they are path-connected; these subsets are the intervals of![]() Also, open subsets of
Also, open subsets of![]() or
or![]() are connected if and only if they are path-connected. Connectedness and path-connectedness are the same for finite topological spaces.
are connected if and only if they are path-connected. Connectedness and path-connectedness are the same for finite topological spaces.
An open set may or may not be path connected, but the closure of an open connected set is also path connected, since all closure does is include the limit points. Path connectedness is a topological property preserved by homeomorphisms. In particular, a homeomorphisms preserves the number of path connected components.
