Theorem
Every complete metric space
is second category.
Proof
A topological space
is said to be first category if
is the countable union of nowhere dense subsets of
All other topological spaces are said to be second category.
Let
be first category. By definition then,
where each
is a nowhere dense subset of
Since
is nowhere dense in
there exists
and
such that
so
is open and
is nowhere dense inso there exist
such that
and
Set
then
and
In this way we obtain a nested sequence of of closed sets
such that fo
and
Hence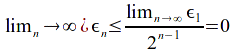
and
exists such that
Also
for every
and
Thusis second category.