Theorem
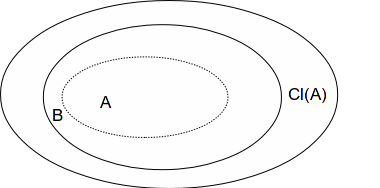
If
is a connected subset of
and there exists a set
such that
then is connected.
Proof
Supposeis disconnected, then
for sets
for open sets
and
Sinceis a connected subset of
either
or
Suppose
then
is closed and
hence
This contradictshenceis connected.