Proof That Any Open Connected Subset of Rn is Polygonally Connected

Theorem

Ifis an open connected subset ofthenis polygonally connected.

Proof

Supposeis open and connected and

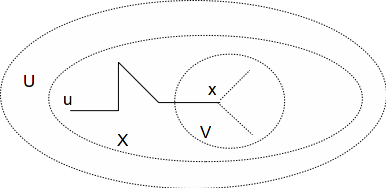
Letbe all points ofwhich can be polygonally connected to

Then

Let

Sinceis open for anythere is an open neighbourhoodofsuch thatcan be polygonally connected to any point ofhencehenceis open.

The setconsists of elements which cannot be polygonally connected tosois

open.

Hence

whereandare disjoint open subsets ofSinceis connected, we have either

or

but sincesoandis polygonally connected.