Proof That a One to One Continuous Function From a Compact Space into a Hausdorff Space is a Homeomorphism

Theorem

Letbe one to one continuous functionfrom a compact spaceinto a Hausdorff space

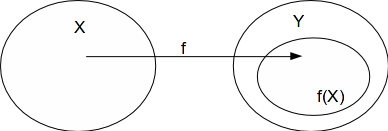
is homeomorphic to

Proof

is a continuous bijection, hence one to one and onto. Henceexists and is well defined.

is continuous if, for every closed subsetofis a closed subset of

Letbe a closed subset of a compact space, thenis compact. Sinceis continuous is a compact subset ofis Hausdorff, since it is a subspace of a Hausdorff space, henceis closed andis continuous.

Henceis a homeomorphism.