Theorem
Polygonally connected subspaces of![]() is path connected.
is path connected.
Proof
Let![]() be polygonally connected and let
be polygonally connected and let![]()
Since![]() is polygonally connected, there are points
is polygonally connected, there are points![]() such that
such that![]()
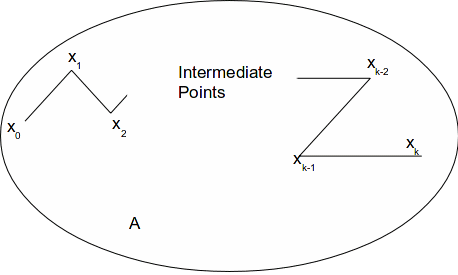
The set![]() is a path. A continuous function
is a path. A continuous function![]()
Hence A is path connected.
Theorem
Polygonally connected subspaces of![]() is path connected.
is path connected.
Proof
Let![]() be polygonally connected and let
be polygonally connected and let![]()
Since![]() is polygonally connected, there are points
is polygonally connected, there are points![]() such that
such that![]()

The set![]() is a path. A continuous function
is a path. A continuous function![]()
Hence A is path connected.