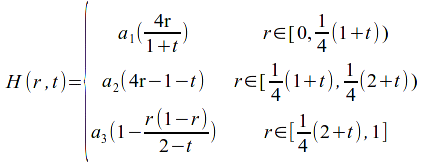Proof That Associativity is Preserved on Homotopy Classes
Theorem
is an equivalence relation on a set
for the set of loops with the same base point
with
if
isloop inhomotopic to a loop
andand
have the same base point
The set of homotopy classes is then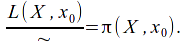
Associativity on the set of homotopy classes, written
is preserved, so that
Proof
Let
be any three equivalence classes in
By definition,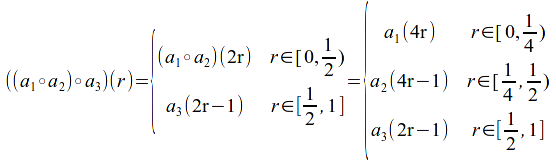
and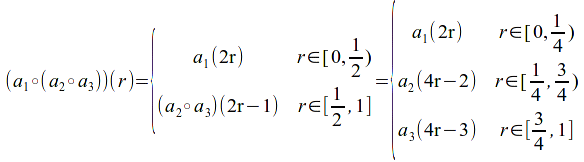
The homotopy between
and
is defined as
