Theorem
A subspace of a completely regular space is completely regular.
Proof
Let
be a completely regular space and let
be a subspace.
Let
be closed in
and let
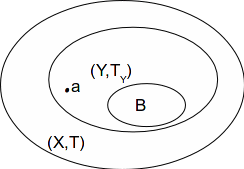
Then
for some
closed in
Since
and
we have
Sinceis completely regular a continuous function
exists such that
and
for
Then
is continuous with
and for
Thenis completely regular.