Theorem
Let![]() be a connected set and let
be a connected set and let![]() be an open cover of
be an open cover of![]() Any two points of
Any two points of![]() can be joined by a simple chain consisting of elements of
can be joined by a simple chain consisting of elements of![]() .
.
Proof
Subsets![]() of
of![]() are said to form a simple chain between points
are said to form a simple chain between points![]() and
and![]() if
if
-
Only
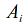 contains
contains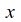
-
Only
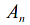 contains
contains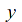
-
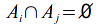 if
if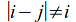
Let![]() and let
and let![]() be the set of all points of
be the set of all points of![]() which are to be joined to
which are to be joined to![]() by a simple chain consisting of elements of
by a simple chain consisting of elements of![]()
Let![]() then there exists a simple chain
then there exists a simple chain![]() from
from![]() to
to![]() All elements of
All elements of![]() belong to
belong to![]() since the chain
since the chain![]() connects x with any element of
connects x with any element of![]() hence
hence![]()
Since![]() is open, so is
is open, so is![]()
Suppose now that![]() Since
Since![]() is a cover of
is a cover of![]() there is an element
there is an element![]() such that
such that![]()
Suppose![]() then there is some chain from
then there is some chain from![]() to
to![]() and
and![]() - a contradiction hence
- a contradiction hence![]() and
and![]()
Hence![]() is open and
is open and![]() is closed.
is closed.
We concude![]() and the theorem is proved.
and the theorem is proved.
