Proof that Equivalence Classes Are Well Defined For The Set of Loops On a Space

Theorem

is an equivalence relation on a setfor the set of loops with the same base pointwithifis a loop inhomotopic to a loopandandhave the same base point

The set of homotopy classes is then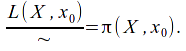

The homotopy class of the loopis written

With this definition,is well defined.

Proof

Let

is a loop with base pointproved here, hence an element of

Ifthen a continuous functionexists such thatand

Define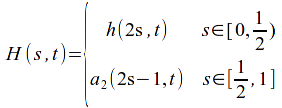

Then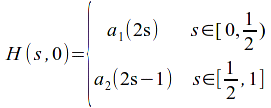

and

Also

Hence

Similarly, if

Henceand

Hence

Then