Theorem
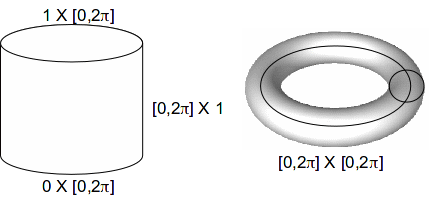
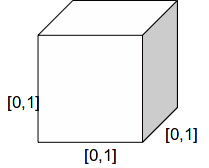
The cylinder, torus and cube are compact spaces.
Proof
The cube is homemorphic to the product space
in
with the usual Euclidean topology.
is compact in
with the usual Euclidean topology. Use Tchonoff's Theorem then the product spaceand the cube are compact.
The torus and cylinder are homeomorphic to the product spaces
and
respectively, hence both are compact by Tychonoff's Theorem.
