Proof That The Homotopy Property With Given Base Point is an Equivalence Relation

Theorem

Letbe the set of all loops inwith base pointThe relation 'homotopic relative tolabelled bydefined onis an equivalence relation.

Proof

since we can definesuch thatfor all

since ifthere exists a continuous functiosuch thatso definethenand sois continuous sinceis.

Ifthere existssuch thatifthere existssuch that

Define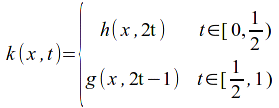

Thenandandis continuous hence