Proof That Two Loops Can Be Joined to Make a New Loop

Theorem

Letbe the set of all loops inwith base pointFor loopsdefine an operationas follows:

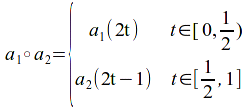
Then

Proof

is formed by travelling around the loopsand then the loop

is continuous onsinceis continuous onandis continuous onand at(is the start and end point for each loop).

Alsoand

Hence