Canonical Transformations

Coordinate transformations or changes of variables are useful because a suitable choice of coordinates or variables can dramatically simplify a problem. For examplecannot be evaluated by inspection but on usingthe integral becomeson using the original substitution to express in terms of

Many integrals can be evaluated in this way by finding a symmetry of the problem and using a substitution which expresses this symmetry. Problems involving circular motion are best expressed in polar co0rdinates therefore and the motion for the electron around a hydrogen atom is best expressed in spherical polar coordinates because the electrostatic potential is spherically symmetrical.

The choice of a generalised coordinate q leads to the expression for the Lagrangian and to the Hamiltonian via the Legendre transformation, with the generalised momentum defined asThe choice ofis arbitrary and any single valued choice ofwill give rise to the same Lagrangian and Hamiltonian equation of motion. We can often make the resulting equations simpler by making using transformed coordinatewhere bothand(the new coordinates) are functions of p and q (the old coordinates). If we could for example find coordinatessuch that the Hamiltonian is a function ofonly then the resulting system would be trivial to solve.

Unfortunately however not all transformations of this type preserve Hamilton's equations of motion so the system may not be Hamiltonian after the transformation. Those which preserve Hamilton's equations of motion have the property that the transformation matrix between the two coordinate systems has a constant determinant:

and

Then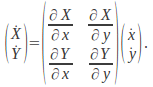

Obviously if the Jacobian matrixhas a constant non zero determinant then uniquedetermines a uniqueand the transformation is well defined. In Ifthen the transformation is said to be canonical and area is preserved for any curve in the phase diagram.