\[l\]
, and allowed to vibrate horizontally.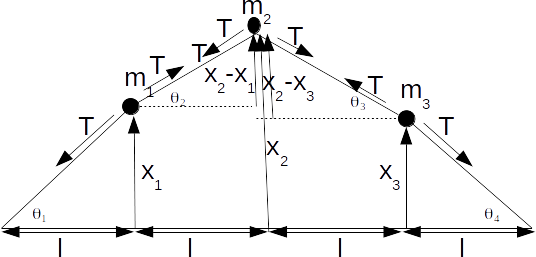
\[x_1, \: x_2\]
and \[x_3\]
respectively. If the increase \[x_1\]
in the length of string 1 is small then we can treat \[T\]
as constant. Resolving vertically for each particle in turn:
Particle 1: \[m_1 \ddot{x}_1= -Tsin \theta_1 +T sin \theta_2\]
Particle 2:
\[m_2 \ddot{x}_2= -Tsin \theta_2 -T sin \theta_3\]
Particle 2:
\[m_3 \ddot{x}_3= Tsin \theta_3 -T sin \theta_4\]
For each
\[x\]
small \[tan \theta =\frac{x}{l} \simeq \theta\]
so the above equations becomeParticle 1:
\[m_1 \ddot{x}_1= -\frac{Tx_1}{l} +\frac{T(x_2-x_1}{l}\]
Particle 2:
\[m_2 \ddot{x}_2= -\frac{T(x_2-x_1)}{l} -\frac{Tx_2-x_3)}{l}\]
Particle 2:
\[m_3 \ddot{x}_3= T\frac{x_2-x_3}{l} - \frac{x_3}{l}\]
Dividing by
\[m_1, \: m_2, \: m_3\]
respectively and writing in matrix form gives\[ \begin{pmatrix}\ddot{x}_1 \\ \ddot{x}_2 \\ \ddot{x}_3 \end{pmatrix} = \left( \begin{array}{ccc} -\frac{2T}{m_1l} & \frac{T}{m_1l} & 0 \\ \frac{T}{m_2l} & -\frac{2Tx_2}{m_2l} & \frac{T}{m_2l} \\ 0 & \frac{T}{m_3l} & - \frac{T}{m_3l} \end{array} \right) \begin{pmatrix}x_1 \\ x_2 \\ x_3 \end{pmatrix} \]
The eigenvalues of the matrix are
\[\lambda\]
and frequencies of vibration are \[f=2 \pi \sqrt{- \lambda}\]
. 