The Uniqueness Theorem

The functionwhich is a solution to Laplace's or Posson's equation and satisfies the boundary conditions is the only function which has these properties, because it is found by integrating Laplace's or Poisson's equation in a methodical manner. Unfortunately for a general distribution of charge, systematic integration is not possible. However suppose that in some region we have found a solution that satisfies the boundary conditions. Then this is the only possible solution.

The uniqueness of the solution for Laplace's equation is easy to prove by considering the potential inside a cavity in a piece of conducting material. The potential on the boundary of the cavity is constant,say. If there is no charge in the cavity, the potential inside it must obey Laplace's equation,One solution of this equation isthroughout the cavity. This is the only solution, for if there were another, saythenmust have a minimum or maximum inside the cavity sinceon the walls but there must be at least one point whereBut solutions of Laplace's equation cannot have minima or maxima. At a maxima for example,see diagram below

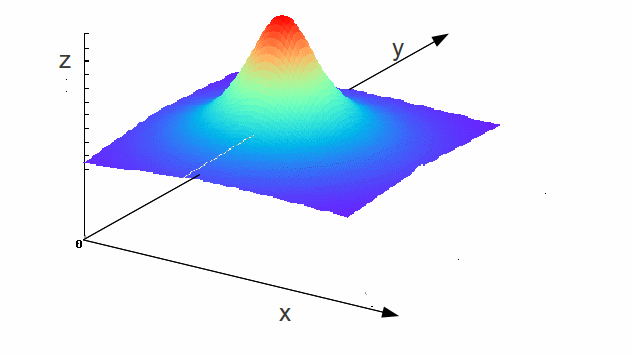
which illustrates whyandin two dimensions, with an obvious extension to three dimensions - but this contradicts that

The uniquess theorem for Poisson's equation can be proved by assuming thatandare both solutions with the same boundary values. The differencemust be zero on the boundary and must satisfy Laplace's equation everywhere. One solution to Laplace's equation withon the boundary iseverywhere and this is the only possible solution. It follows that there cannot be two solutionandsatisfying the same boundary conditions and the uniqueness theorem holds for Poisson's equation too.