Fixed Points, Equilibrium and Stability

The fixed points of a dynamical system are the roots of the equation vec v =0. We can find the fixed points by solving this system of equations and linearising the system about the fixed point. We can find the eigenvalues and eigenvectors of the associated matrix and these eigenvalues and eigenvectors will determine the nature of the fixed point.

Example: Find and classify the fixed points for the system

We linearise the system

Evaluated atthese become

The matrix representing the linearised system about the fixed point is

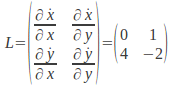
The eigenvalues of this matrix are the solutions to

These eigenvalues are both positive so the fixed pointis unstable.

In general

1. If the eigenvalues are positive for the linearised matrix about a fixed point then the fixed point is unstable.

2. If the eigenvalues are negative for the linearised matrix about a fixed point then the fixed point is stable.

3. If some eigenvalues are negative and some positive for the linearised matrix about a fixed point then the fixed point is neither stable nor unstable.