For first order systems the motion tends to fixed points or infinity, but for second order systems the situation can be more complex. Consider for example a system separable in polar coordinates![]() such that the motion has a fixed point (in terms of
such that the motion has a fixed point (in terms of![]() ) other than at the origin:
) other than at the origin:
![]()
![]()
where![]() are constant.
are constant.
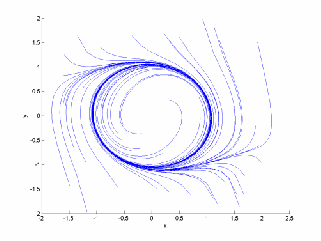
The circle![]() is a phase curve and since the motion moves around it indefinitely it is a cycle. Any closed phase curve is a cycle – a motion for which
is a phase curve and since the motion moves around it indefinitely it is a cycle. Any closed phase curve is a cycle – a motion for which![]() are periodic with the same period.
are periodic with the same period.
For![]() the motion of the system above is a circle and we may treat
the motion of the system above is a circle and we may treat![]() as a fixed point of the system. In the region of
as a fixed point of the system. In the region of![]() the motion obeys the equations
the motion obeys the equations
![]() where
where![]()
![]()
The solution of this linearisation is![]() and the phase curves are given by eliminating
and the phase curves are given by eliminating![]() from these two equations, obtaining
from these two equations, obtaining
![]()
If![]() the system is stable in the sense that motion initially close to the system will be attracted to it, and any perturbed motion initially on the circle will return to it. If
the system is stable in the sense that motion initially close to the system will be attracted to it, and any perturbed motion initially on the circle will return to it. If![]() the system is unstable.
the system is unstable.
A more general form of limit cycle is shown below with various starting points.