The equation of motion for autonomous motion in a circle is
(1) where
is
periodic.
Simple examples include
and
The period
of the motion is the time taken for
to increase byand may be found by rearranging (1) to give
and then integrating:
Motion in a circle may have fixed points and terminating motion just like motion in a line.
Example: Find the fixed points for the motion defined by
for
The fixed points are the solutions of
If
then there are two fixed points at
where
The fixed point at
is stable and the fixed point atis unstable.
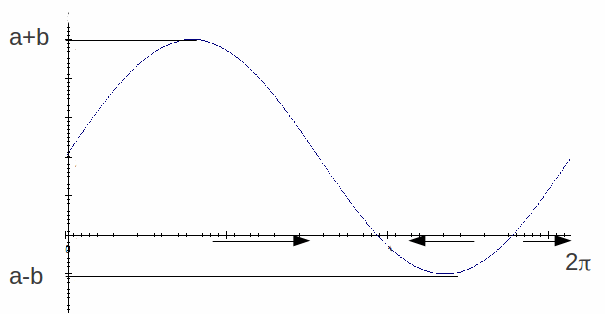
If
there is a single fixed point at
which is neither stable or unstable.
For
there are no fixed points and the motion is purely rotational. The sign of
never changes sign.