Phase Curves and Phase Diagrams

The motion of a dynamical system traces out a curve in phase space called a phase curve. For an autonomous system there is only one phase curve through each point, given by– withanddenoting the initial conditions. Another solutionrepresents the same curve in phase space differently parametrized.

For any autonomous system we may define for eacha transformation of the phase space by

Theorem

The phase flowsatisfies

Proof: For any solution is also a solution whereis any number.

In terms of flows this means

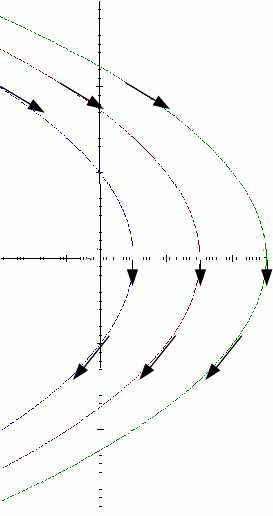
For second order systems we may sketch the the phase diagram in the plane. It is impossible to draw all the phase curves but usually only a representative sample are required. The solution is rarely in closed form, so qualitative methods are required. Often we can find the direction field from the unsolved system and plot them in the plane, joining up the arrows so that the phase curves are continuous.

Example:The y component of velocity is always negative, while the- component increases in magnitude with distance from the– axis, is positive in the top half of the plane and negative below it.