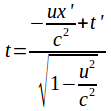A body of length
moving with speed
along the x – axis of an inertial frame O, but at rest in its own rest frame O' will be observed by a stationary observer to be apparently shortened to a length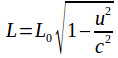
and two events separated by a time interval of length
in the rest frame O' will be observed by the stationary observer in rest frame O to be separated by a longer interval of time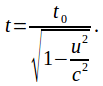
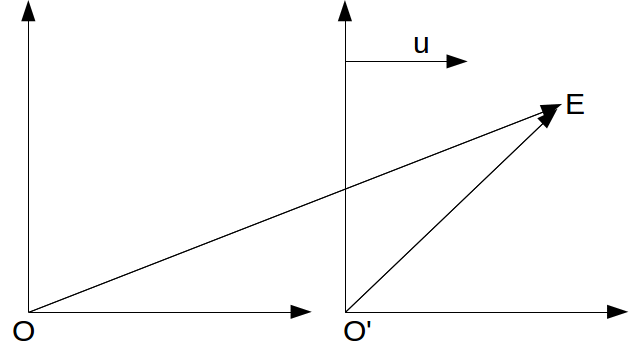
Suppose the two inertial frames O and O' coincide at t=t'=0. At this instant a light pulse is emitted and produces an event E at coordinates
in the inertial frame O and
in the inertial frame O'.
and
are related by
Since O' is moving along the x axis of O,
and
hence
Since light travels in straight lines, the relationship between
and
will be linear so we can write
(1) and
(2)
Since
when light ray is emitted, from (1)
(1) becomes
(3)
Substitute (2) and (3) these expressions into
to get
Equating coefficients of
(4)
Equating coefficients of
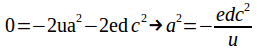(5)
Equating coefficients of
(6)
Square (5) to give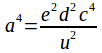
(7)
From (4)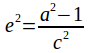
and from (6)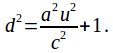
Substitute these into (7) to obtain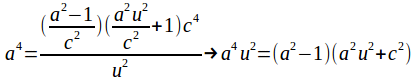
Expanding and simplifying gives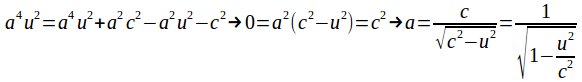
Then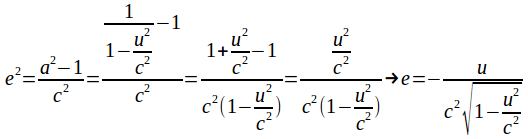
(Take the positive square root so that
and
flow in the same direction).
From (5)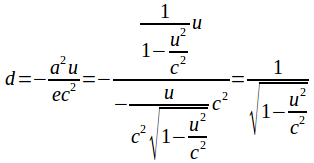
Then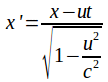
and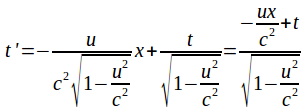
The transformation is symmetrical, so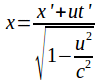
and