In general a trigonometric equation of the form![]() for example may have more than one solution, and may have in fact an infinite number of solutions. We often have to find the solutions within a certain range eg 0 – 360 o or
for example may have more than one solution, and may have in fact an infinite number of solutions. We often have to find the solutions within a certain range eg 0 – 360 o or![]() depending on whether we are working in degrees or radians. All the trigonometric graphs – sin, cos and tan – possess symmetry.
depending on whether we are working in degrees or radians. All the trigonometric graphs – sin, cos and tan – possess symmetry.
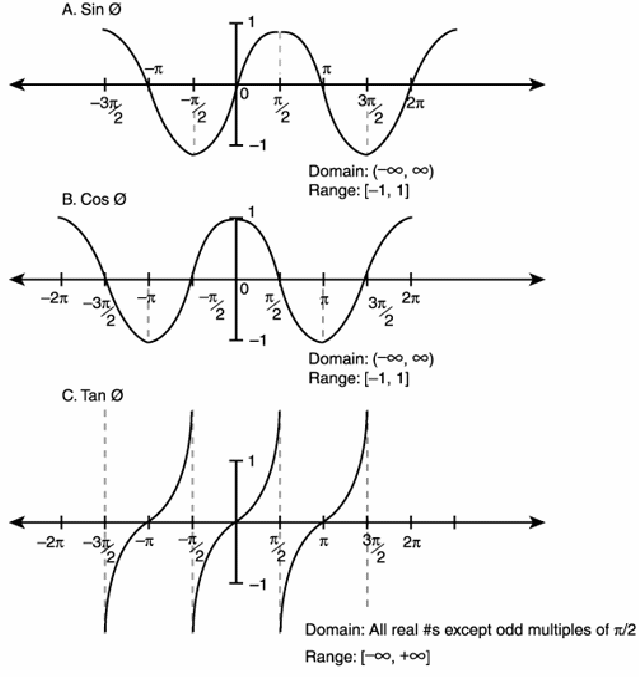
All the graphs repeat every![]() This means that if
This means that if![]() is a solution to a trigonometric equation, then
is a solution to a trigonometric equation, then![]() will also be a solution for any integer n. However there are also specific rules for each function.
will also be a solution for any integer n. However there are also specific rules for each function.
Example:
Solve![]()
![]()
Since sin repeats every![]() and is symmetrical about the lines
and is symmetrical about the lines![]()
![]() are also solutions.
are also solutions.
The complete set of solutions is
![]()
Solve![]()
![]()
Since cos repeats every![]() and is symmetrical about the lines
and is symmetrical about the lines![]()
![]() are also solutions.
are also solutions.
The complete set of solutions is
![]()
Solve![]()
![]()
Since tan repeats every![]() and is not symmetrical about any line
and is not symmetrical about any line![]() are also solutions.
are also solutions.
The complete set of solutions is
![]()
