Any linear system of equations can be written in matrix form, where the matrix is the matrix of coefficients. For example the system
can be written as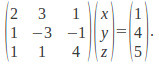
The system can be solved, the solution found by multiplying both sides by the inverse of the matrix,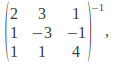
obtaining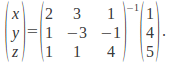
This is only possible if the matrix has an inverse. The matrix has an inverse only if the determinant is non – zero, and the matrix only has a non – zero determinant only if the equations are independent, so that none of the equations can be obtained by adding combinations of the other two.
If the equations are independent in the way described, then the solution is unique, and such a unique solution always exists for a square matrix of coefficients made up of independent equations, where the number of equations is equal to the number of variables.
If the number of equations is LESS than the number of variables, and the equations are independent then in general an infinite number of solutions exist. The solutions can be neatly expressed with the introduction of parameters.
If the number of equations is MORE than the number of variables, the equations cannot be independent. We may be able to reduce the number of equations to form an independent set, possibly obtaining a square matrix so we can solve the system or we may not. If we cannot do this then the system has no solution – it is inconsistent.
For example, consider the system
(1)
(2)
(3)
The system is independent, but (2)-(1) gives
and (3)-(2) gives
– a contradiction. In general though inconsistency results in the same combination of terms being equal to different numbers eg
and