For any particle moving on a flat surface, we can find the position vector relative to a fixed point, by counting to the right x units, up y units and writing down![]() If instead we move to the left or down then
If instead we move to the left or down then![]() or
or![]() are negative. Suppose though that the particle starts from the point
are negative. Suppose though that the particle starts from the point![]() with velocity
with velocity![]() After
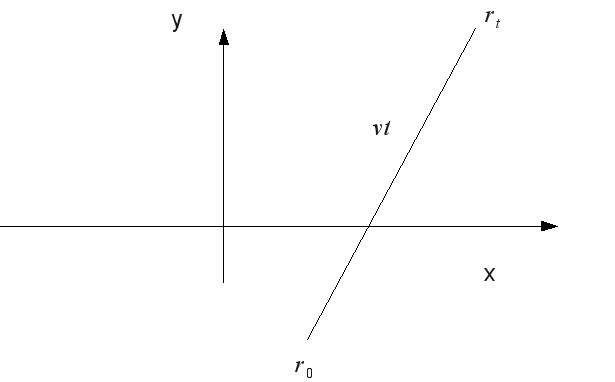
After![]() seconds it will have moved by a vector
seconds it will have moved by a vector![]() and it' s new position will be at
and it' s new position will be at![]() This is illustrated on the graph below.
This is illustrated on the graph below.
If we have two particles, A and B, both moving Then the position vector of B relative to A is given by![]()
If![]() then the position vector of B relative to A is given by
then the position vector of B relative to A is given by
![]()
and the velocity of B relative to A is![]() . If the velocities of both particles are constant, as in this case then the relative velocity is constant.
. If the velocities of both particles are constant, as in this case then the relative velocity is constant.
If particle A is initially at![]() moving with velocity
moving with velocity![]() and B is at
and B is at![]() at the same time, moving with velocity 9i+10j the the position vector of A at any time is
at the same time, moving with velocity 9i+10j the the position vector of A at any time is![]()
The position vector of B relative to A is![]() and the velocity of B relative to A is
and the velocity of B relative to A is![]()
