\[m\]
along a rough horizontal surface with coefficient or friction \[\mu\]
?Let
\[F\]
be a force at \[\theta\]
to the horizontal and let \[R\]
be the normal reaction force.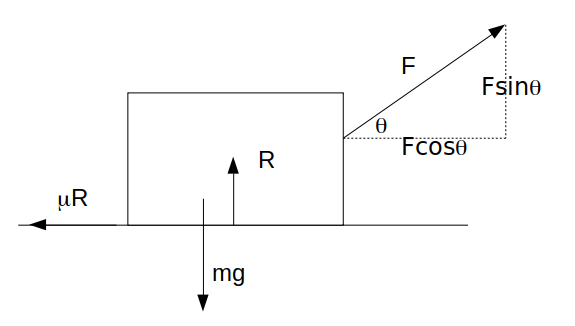
\[\mu R =F cos \theta\]
\[R +F sin \theta =mg \rightarrow R=mg-F sin \theta\]
The first divided by the second gives
\[\mu = \frac{F cos \theta }{mg- F sin \theta}\]
.Solving for
\[F\]
gives \[F= \frac{ \mu mg}{\mu sin \theta + cos \theta }\]
.To find the minimum value of
\[F\]
note that the numerator is fixed, so we must maximise the denominator. This is maximum when \[\frac{d}{d \theta } (\mu sin \theta + cos \theta)= \mu cos \theta - sin \theta = 0\]
.Hence
\[sin \theta = \mu cos \theta \rightarrow tan \theta = \mu\]
.The minimum force is
\[F= \frac{\mu mg}{cos \theta ( 1+ \mu tan \theta )}= \frac{ \mu mg sec \theta}{ 1+ \mu^2} = \frac{ \mu mg \sqrt{1+ tan^2 \theta}}{1+ \mu^2}= \frac{ \mu mg \sqrt{1+ \mu^2}}{1+ \mu^2}= \frac{ \mu mg}{\sqrt{1+ \mu^2}}\]
. 