Hypothesis Testing for the Equality of the Means of Two Populations if the Common Variance is not Known

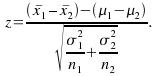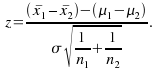When independent samples of sizeandaretaken from two normally distributed populations with meansand andknown population standard deviationsandtherandom variableisnormally distributed with meanandvariance isnormally distributed. We can test for the equality ofandbydoing a hypothesis test usingIfthen(1)

Ifisnot known then we cannot use the last expression above. We canhowever work out an estimate for the varianceusingthe sample variancesandWecan use these as two estimates ofandpool them by weighting them according to their sample size or degreesof freedom:

so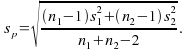

Replacingin(1) with the pooled standard deviationgivesthe random variable 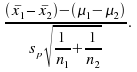whichhas adistributionwithdegreesof freedom.

The assumptionmustbe made but in practice we can use this test ifandarenot dissimilar – they do not differ by a factor of more than about2.

Example: Test for the equality of the two means of the two sets ofdata at the 10% level:

A: 51.4, 76.7, 73.7, 66.2, 65.5, 49.7, 65.8, 62.1, 75.8, 62.0,72.0, 55.0, 79.7, 65.4, 73.3

B: 86.0, 59.7, 68.6, 98.6, 87.7, 69.0, 80.2, 78.1, 69.8, 77.2

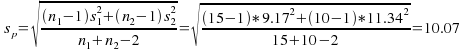
No assumption is made as two which is greater so we carry out atwo tailed test:

and

Reject the null hypothesis.