The sampling distribution for the variance of a normaldistribution with variance![]() isgiven by
isgiven by ![]()
This means that if a random sample of size![]() istaken from a normally distributed population with variance
istaken from a normally distributed population with variance![]() thenthe random variable
thenthe random variable![]() hasthe
hasthe![]() distributionwith
distributionwith![]() degreesof freedom.
degreesof freedom.
To perform a hypothesis test for the hypothesis![]()
Is the population normal?
State the null hypothesis
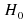 – that
– that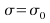 -and the alternative hypothesis
-and the alternative hypothesis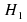 –that
–that 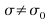 fora two tailed test OR that either
fora two tailed test OR that either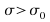 OR
OR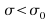 fora one tailed test.
fora one tailed test.Find the test statistic
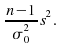 Comparethis with the values of
Comparethis with the values of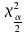 -two tailed test – or
-two tailed test – or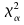 -if
-if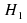 is
is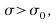
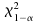 if
if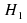 is
is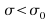 -from the
-from the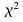 tables.
tables.Reject
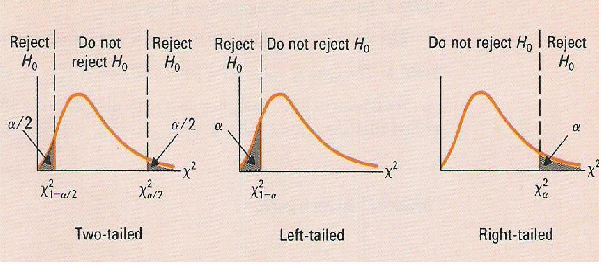
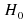 ifthe test statistic falls into any of the shaded regions in thediagram below, else do not reject
ifthe test statistic falls into any of the shaded regions in thediagram below, else do not reject
Example: Conduct a hypothesis test at the 95% level to testwhether the variance of the population from which this sample istaken
3,4,3,4,5,6,2,3,4,5
is equal to 1.
Null Hypothesis,![]()
Alternative Hypothesis,![]()
![]()
The test statistic is![]()
![]() and
and![]()
We do not reject![]()
